Función Matemática
Una función es una regla de correspondencia entre
dos conjunto de
tal manera que a cada elemento del primer conjunto le corresponde uno y sólo un
elemento del segundo conjunto.
- Al primer conjunto (el conjunto D) se le da el nombre de dominio.
- Al segundo conjunto (el conjunto C) se le da el nombre de contra- dominio o imagen.
Por otra parte una función se puede concebir
también como un aparato de calculo. La entrada es el dominio, los
cálculos que haga el aparato con la entrada son en sí la función y la salida
sería el contra dominio.
Esta forma de concebir la función facilita el
encontrar su dominio.
Notación: al número que "entra" a la
máquina usualmente lo denotamos con una letra, digamos  o
o cualquier
otra.
cualquier
otra.
 o
o cualquier
otra.
cualquier
otra.
A este respecto Una función también vista como
una «Caja Negra», que transforma los valores u objetos de «entrada» en los valores u
objetos de «salida»
En matemática , se dice que una magnitud o cantidad es función de otra si el valor de la
primera depende exclusivamente del valor de la segunda. Por ejemplo el área A de un circulo es función de su radio: el valor del área es proporcional al cuadrado del radio, A = π·r2.
Del mismo modo, la duración T de un viaje de tren entre dos
ciudades separadas por una distancia d de 150 km depende de la velocidad v a la que este se desplace: la
duración es inversamente proporcional a la velocidad, T = d / v.
A la primera magnitud (el área, la duración) se la denomina variable dependiente y la cantidad de la que depende (el radio, la velocidad) es la variable independiente. El concepto general de función, aplicación o mapeo se refiere en matemáticas a
una regla que asigna a cada elemento de un primer conjunto un único elemento de
un segundo conjunto. Por ejemplo, cada número entero posee un único cuadrado, que resulta ser un número natural (incluyendo el cero)
Para entender un poco más de
funciones hay que saber los
conceptos de Dominio y Rango :
En matemáticas , el dominio (conjunto de definición o
conjunto de partida) de una función es el conjunto de existencia de la misma,
es decir, los valores para los
cuales la función está definida. Es el conjunto de todos los objetos que puede
transformar, se denota o bien.
Son todos los valores posibles de f(x) o sea de
Y. Si tenemos f(X) = sen (X) El rango va de -1 a +1.
Si F(X) = una parábola cóncava en forma de U. El
rango va del vértice dala parábola hacia arriba hasta + infinito.
La manera habitual de denotar una función f es:
f: A → B
a → f(a),
Donde A es
el dominio de la función f, su primer conjunto
o conjunto de partida; e B es
el dominio algoritmo para
obtener la imagen de un cierto objeto arbitrario a del dominio A, es decir, el (único) objeto de B que le corresponde. En
ocasiones esta expresión es suficiente para especificar la función por
completo, infiriendo el dominio y codominio por el contexto. En el ejemplo
anterior, las funciones «cuadrado» e «inicial», llámeseles f y g, se denotarían entonces como:
f: Z → N
k → k2, o sencillamente f(k) = k2;
g: V → A
p →
Inicial de p;
si se conviene V = {Palabras del español} y A = {Alfabeto español}.
Una función puede representarse de diversas formas:
mediante el citado algoritmo para obtener la imagen de cada elemento, mediante
una tabla de valores que empareje cada valor de la variable independiente con
su imagen —como las mostradas arriba—, o como una gráfica que dé una imagen de la función.
Ejemplo: Sea X={A,B,D,Z}
Y={4,6,7,8,9} y la función fx -> y
cuya gráfica es:
(A, 7) (B, 4) (D, 9) (Z, 8)
Conjunto de partida {A, B, D, Z}
DOMINIO f: {A,
B, D, Z}
RANGO: {4,6,7,8,9}
Variable Independiente: Es
la X
Variable dependiente: Es la
Y
Ejemplo:
Y=2X-6
- se sustituye la X por cada uno de los valores que se le desea dar
solución:
X=-3
Y=-2(-3)-6
Y=-6-6
Y=-12
X=-1
Y=-2(-1)-6
Y=-2-6
Y=-8
X=2
Y=2(2)-6
Y=4-6
Y=-2
X=4
Y=4(2)-6
Y=8-6
Y=2
Rango f = Todos los Reales " R"
dominio f =Todos los Reales " R"
PROPUESTOS : Dadas las funciones
A )f (X)= X-3
B) f(X)= -3X+1/4
C) f(X)= X-6
Hallar Dominio, Rango y Gráficar
Tipos de Funciones
Funciones algebraicas
En esta función las operaciones que hay que efectuar con la variable
independiente son: la adición(+), sustracción(-), multiplicación(*), división(/),
potenciación(an) y radicación.
Las Funciones Algebraicas pueden ser:
- Funciones explícitas
Si se pueden obtener
las imágenes de x por simple sustitución.
f(x) = 5x
− 2
- Funciones implícitas
Si no se pueden
obtener las imágenes de x por simple sustitución, sino que es preciso efectuar
operaciones.
5x − y − 2
= 0
Funciones Polinómicas
las funciones Polinómicas son las que vienen definidas por un polinomio.
f(x) = a0 + a1x + a2x² + a2x³ +···
+ anxn
Su dominio es  , es
decir, cualquier número real tiene imagen.
, es
decir, cualquier número real tiene imagen.
Funciones constantes
El
criterio viene dado por un número real.
f(x)=
k
La gráfica es una recta horizontal paralela a
al eje de abscisas.
Funciones polinómicas de primer grado
f(x)
= mx +n
Su gráfica es una recta oblicua, que queda
definida por dos puntos de la función.
Funciones a trozos
Son funciones
definidas por distintos criterios, según los intervalos que se consideren.
Funciones radicales
- El criterio viene dado por la variable x bajo el signo radical.
- El dominio de una función irracional de índice impar es R.
- El dominio de una función irracional de índice par está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.
Funciones trascendentes
La
variable independiente figura como exponente, o como índice de la raíz, o se
halla afectada del signo logaritmo o de cualquiera de los signos que emplea la
trigonometría.
función Lineal
La función lineal es una función polinómica de primer grado; dicho de otro, es una función cuya representación en el plano cartesiano es una línea recta. Esta función se puede escribir como:
-
-
cuando b es distinto de cero.
Ejemplo:
Una función lineal de una única variable dependiente x es de la forma:
En la ecuación:
En una recta el valor de m se corresponde al ángulo de inclinación de la recta con el eje de las x a través de la expresión:
de inclinación de la recta con el eje de las x a través de la expresión:

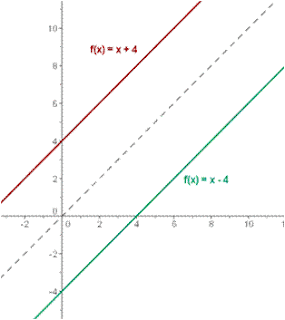
- que se conoce como ecuación de la recta en el plano xy.
- En la figura se ven dos rectas, que corresponden a las ecuaciones lineales siguientes:
En la ecuación:
En una recta el valor de m se corresponde al ángulo
 de inclinación de la recta con el eje de las x a través de la expresión:
de inclinación de la recta con el eje de las x a través de la expresión:
visita esta pagina web donde encontraras la definición de función lineal y una manera mas sencilla de aprender realizando ejercicios..... Has Clic en el ENLACE
Función Cuadrática
En matemáticas, una función cuadrática o función
de segundo grado es una función polinómica definida como: 

Donde a, b y c son números reales (constantes) y a es distinto de 0.
La representación gráfica en el plano cartesiano de una función cuadrática es una parábola, cuyo eje de simetría es paralelo al eje de las
ordenadas. La parábola se abrirá hacia arriba si el signo de a es positivo, y hacia abajo en caso
contrario. El estudio de las funciones cuadráticas tiene numerosas aplicaciones
en campos muy diversos, como por ejemplo la caída libre o el tiro parabólico.
Las raíces (o
ceros) de una función cuadrática, como en toda función, son los valores de x, para los cuales  Por tratarse de un polinomio de grado 2, habrá a lo
sumo 2 raíces, denotadas habitualmente como:
Por tratarse de un polinomio de grado 2, habrá a lo
sumo 2 raíces, denotadas habitualmente como: y
y  dependiendo del valor del discriminante Δ
definido como:
dependiendo del valor del discriminante Δ
definido como:
 Por tratarse de un polinomio de grado 2, habrá a lo
sumo 2 raíces, denotadas habitualmente como:
Por tratarse de un polinomio de grado 2, habrá a lo
sumo 2 raíces, denotadas habitualmente como: y
y  dependiendo del valor del discriminante Δ
definido como:
dependiendo del valor del discriminante Δ
definido como:
§ Dos soluciones reales y diferentes si el discriminante es
positivo:
§ Una solución real doble si el
discriminante es cero:
- Dos números complejos conjugados si el discriminante es negativo:
Representación
analítica
Existen tres formas principales de escribir una
función cuadrática, aplicables según el uso que se le quiera dar a la función:
un estudio analítico de la función o de la ecuación cuadrática, una
interpretación o construcción geométrica de la parábola, etc. Las tres formas
son equivalentes.
Forma
desarrollada
La forma desarrollada de una función cuadrática (o forma
estándar) corresponde a la del polinomio de segundo grado, escrito
convencionalmente como:
Forma
factorizada
las cuadráticas se pueden escribir de forma
factorizada en función de sus
raíces como:
Siendo a el coeficiente principal de la
función, y  y
y  las raíces de f(X) . En el caso de que el discriminante Δ sea igual a 0 entonces
las raíces de f(X) . En el caso de que el discriminante Δ sea igual a 0 entonces por lo que la factorización adquiere la forma:
por lo que la factorización adquiere la forma:
 y
y  las raíces de f(X) . En el caso de que el discriminante Δ sea igual a 0 entonces
las raíces de f(X) . En el caso de que el discriminante Δ sea igual a 0 entonces por lo que la factorización adquiere la forma:
por lo que la factorización adquiere la forma:
Representación gráfica
Corte con el eje y
La función corta el eje y en el punto y = f(0), es decir, la
parábola corta el eje y cuando x vale cero (0):
lo que resulta:
La función corta el eje y en el punto (0, c), siendo c el término independiente de la
función.
A este punto de la función también se lo
conoce con Ordenada al Origen.
Corte
con el eje x
La función corta al eje x cuando y vale 0, dada la función:
Se tiene que:
las distintas soluciones de esta ecuación de segundo grado, son los casos de corte
con el eje x, que se
obtienen, como es sabido, por la expresión:
Ejemplo: dada la función f(X)=X2+3X-4 hallar dominio, rango y gráfica de la función:
solución
a=1>0(hacia arriba)
a=1
b=3
c=-4
vértice
Yv=(-3/2)2 + 3 (-3/2)-4
Yv=-9/4 -9/2 -4
Yv= -25/4
V=(-3/2 , -25/4)
Cortes con los ejes
Corte con el eje Y, hacer X=0
Y= X2+3X-4
Y=(0)2+3(0)-4
Y=-4
Corte con el eje X hacer Y=0
factorización
X2+3X-4 = 0 ->(X-1) (X+4)=0
m.n=-4
-1.4=-4
m+n=3
-1+4=3
X-1=0 y X+4=0
X1 X=-4
son las raíces. luego de tener los cortes se procede a gráfica la Parábola queda hacia arriba.
PROPUESTOS
Dada las funciones hallar dominio, rango y gráfica de las mismas.
- f(X) =1-X2
- 3X2-4X+1
- X2-25
-X2
En los siguientes vínculos encontraras mas Información a cerca de las Funciones Cuadráticas.
Función Exponencial
La función exponencial es del tipo:
Sea a un número real
positivo. La función que a cada número real x le hace
corresponder la potencia ax se llama función
exponencial de base a y exponente x. También se puede decir que la función exponencial es conocida formalmente como la función real ex, donde e es el número
de Euler, aproximadamente 2.71828...; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la
particularidad de que su derivada es la misma función. Se denota
equivalentemente como f(x)=ex o exp(x), donde e es la base de los logaritmos naturales y
corresponde a la función
inversa del logaritmo
natural.
En términos mucho más generales,
una función real E(x)
se dice que es del tipo
exponencial en base a si tiene la forma
ex ->2,71828
Ejercicio: (x)=ex3 +3
f(x)=e(-1)3 +3
f(-1)e2
f(-1)e=2,712
f(-1)=7,38
La gráfica queda de esta manera:
PROPUESTOS
1 
2 
3
4
5
6
7
8
9
10
11
12
13
14

has clic en los siguientes link y encontrarás mas información acerca de las funciones exponenciales.
función Cubica
La
función cúbica es una función polinómica de tercer grado. Tiene la
forma: ; donde el coeficiente a es distinto
de 0.Tanto el dominio de definición como el conjunto imagen de estas funciones pertenecen a los números reales
La derivada de una
función cúbica genera una función cuadrática y su integral una función
cuártica.
; donde el coeficiente a es distinto
de 0.Tanto el dominio de definición como el conjunto imagen de estas funciones pertenecen a los números reales
La derivada de una
función cúbica genera una función cuadrática y su integral una función
cuártica.
Un ejemplo de función cúbica es: y = f(x) = x3,
es la llamada: parábola cúbica
Propiedades:
§ El dominio
de la función es la recta real es decir (-α : α)
§ El
recorrido de la función es decir la imagen es la recta real.
§ La función
es simétrica respecto del origen, ya que f(-x)=-f(x).
§ La función
es continua en todo su dominio.
§ La función
es siempre creciente.
§ La función
no tiene asintotas.
§ La función
tiene un punto de corte con el eje Y.
§ La función
puede tener hasta un máximo de 3 puntos de intersección con el eje X.
Ejemplo:
Grafíque y analice las propiedades de la siguientes funciones
a) f(x) = 2x3 +
3x2 - 12x=o
Propidades
§ Dominio:
El conjunto de los Reales
§ Imagen: El
conjunto de los Reales
§ Ceros de
la función:
Se iguala la función a cero
2x3 + 3x2 - 12x = 0 x( 2x2 + 3x - 12) = 0 Extrayendo factor común
x = 0 ( 2x2 + 3x +
12)= 0 Igualando a cero ambos factores y realizar la descomposición.
§ Simetría:
Demostrar que cumple f(-x)=-f(x).
Para demostrar la simetría analíticamente de selecciona un número
cualesquiera y su opuesto ejemplo 1 y -1 Demostrar que f(-1) = - f(1)
f(-1) = 2(-1)3 +
12 . (-1)2 + 2. (-1 )
= 2.(-1) + 12 . 1 - 2
= -2 + 12 - 2
= 10 - 2
= 8
f(1) = 2(1)3 +
12 . (1)2 + 2. (1 )
= 2.(1) - 12 . 1 + 2
= 2 - 12 + 2
= -10 + 2
= -8
Como f(-1) = - f(1) por tanto la función es simétrica.
§ Continuidad:
La función es continua en todo su dominio pues gráficamente se puede observar
que no tiene ningún punto de discontinuidad.
§ La función
no tiene asuntotas.
§ Para
determinar los puntos donde la función corta el eje de la y
Se determina el valor de la función para x=0 f(0) = 2. 03 + 3. 02 - 12. .0 Obteniendo y= 0 y la función
corta el eje de la y en el punto (0:0)
b) F(x) = -x3 +8
propuestos
Grafique y analice las siguientes funciones cúbicas.
1) f(x) = x3 + 12x + 2
2) f(x) = -x3 + 3x2 + 9x
3) f(x) = 3x2 + x3 - 1
función Racional
La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.
Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.
FUNCIÓN INVERSA
Se llama función inversa o reciproca de f a otra función f−1 que cumple que:
Si f(a)
= b, entonces f−1(b) = a.
Podemos observar que:
El dominio
de f−1 es el recorrido de f.
El
recorrido de f−1 es el dominio de f.
Si queremos hallar el recorrido de una
función tenemos que hallar el dominio de su función inversa.
Si dos funciones son inversas su composición es la función identidad.
f o f −1) (x) = (f −1 o f) (x) = x
Las gráficas de f y f -1 son simétricas respecto de la bisectriz del
primer y tercer cuadrante.
hacer clic en el vinculo










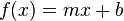




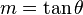






























No hay comentarios:
Publicar un comentario